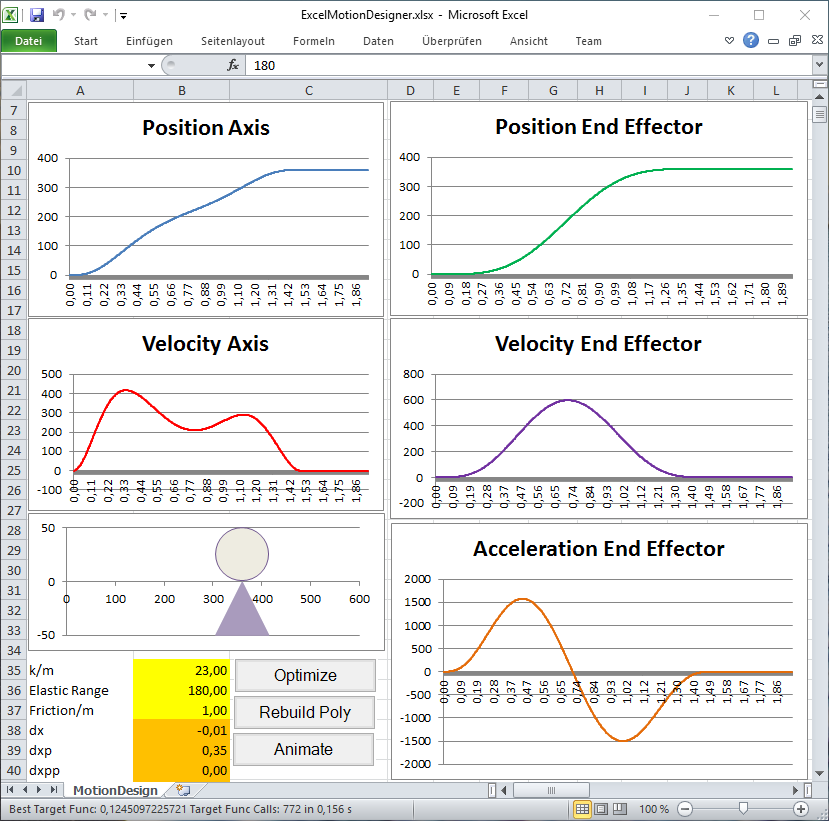
Polynomial Splines can be used to automatically generate countervibrations in order to damp an end effector vibration.
In the example shown below the end effector (circle shaped) and the axis (triangle shaped) describe an oscillating system.
 Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube. PGRpdiBjbGFzcz0iX2JybGJzLWZsdWlkLXdpZHRoLXZpZGVvLXdyYXBwZXIiPjxpZnJhbWUgbG9hZGluZz0ibGF6eSIgd2lkdGg9IjU2MCIgaGVpZ2h0PSIzMTUiIHNyYz0iaHR0cHM6Ly93d3cueW91dHViZS1ub2Nvb2tpZS5jb20vZW1iZWQvSEcybm90Z3RHRTQ/cmVsPTAmYW1wO3ZxPWhkMTA4MCIgZnJhbWVib3JkZXI9IjAiIGFsbG93PSJhdXRvcGxheTsgZW5jcnlwdGVkLW1lZGlhIiBhbGxvd2Z1bGxzY3JlZW49IiI+PC9pZnJhbWU+PC9kaXY+ |
The video illustrates with two different oscillation ratios how our optimization routines automatically detect a polynomial spline for the movement of the axis so that it is synchronized with the oscillation behavior of the end effector which thereby greatly attenuates. Thus it is achieved that at the same time at the end of the movement the axis and the end effector come to a standstill.
This method allows very flexible damping or even eliminating occurring vibrations, e.g. when handling liquids or generally elastic end effectors. In addition, polynomial splines can be easily mapped to any standard motion control system as cams, so no special operating system is necessary.
|
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube. PGRpdiBjbGFzcz0iX2JybGJzLWZsdWlkLXdpZHRoLXZpZGVvLXdyYXBwZXIiPjxpZnJhbWUgbG9hZGluZz0ibGF6eSIgd2lkdGg9IjU2MCIgaGVpZ2h0PSIzMTUiIHNyYz0iaHR0cHM6Ly93d3cueW91dHViZS1ub2Nvb2tpZS5jb20vZW1iZWQvLTdjVTEwcVdSQzg/cmVsPTAmYW1wO3ZxPWhkMTA4MCIgZnJhbWVib3JkZXI9IjAiIGFsbG93PSJhdXRvcGxheTsgZW5jcnlwdGVkLW1lZGlhIiBhbGxvd2Z1bGxzY3JlZW49IiI+PC9pZnJhbWU+PC9kaXY+ Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube. PGRpdiBjbGFzcz0iX2JybGJzLWZsdWlkLXdpZHRoLXZpZGVvLXdyYXBwZXIiPjxpZnJhbWUgbG9hZGluZz0ibGF6eSIgd2lkdGg9IjU2MCIgaGVpZ2h0PSIzMTUiIHNyYz0iaHR0cHM6Ly93d3cueW91dHViZS1ub2Nvb2tpZS5jb20vZW1iZWQvT2Z6MnFCMktOc1k/cmVsPTAmYW1wO3ZxPWhkMTA4MCIgZnJhbWVib3JkZXI9IjAiIGFsbG93PSJhdXRvcGxheTsgZW5jcnlwdGVkLW1lZGlhIiBhbGxvd2Z1bGxzY3JlZW49IiI+PC9pZnJhbWU+PC9kaXY+ |
powered by Borlabs Cookie