 Viele Prozesse bedingen eine dynamische punktgenaue Umkehrbewegung oder auch ein punktgenaues Überschleifen.
Viele Prozesse bedingen eine dynamische punktgenaue Umkehrbewegung oder auch ein punktgenaues Überschleifen.
Mithilfe unseres Ansatzes über Lineare Splines für die Bewegung und unsere numerischen Solver-Methoden lässt sich eine hochdynamische präzise Bewegung erzielen.
|
PGlmcmFtZSB3aWR0aD0iNTYwIiBoZWlnaHQ9IjMxNSIgc3JjPSJodHRwczovL3d3dy55b3V0dWJlLW5vY29va2llLmNvbS9lbWJlZC92V2RpVWR2SG9Bcz9yZWw9MCZhbXA7dnE9aGQxMDgwIiBmcmFtZWJvcmRlcj0iMCIgYWxsb3c9ImF1dG9wbGF5OyBlbmNyeXB0ZWQtbWVkaWEiIGFsbG93ZnVsbHNjcmVlbj0iIj48L2lmcmFtZT4= |
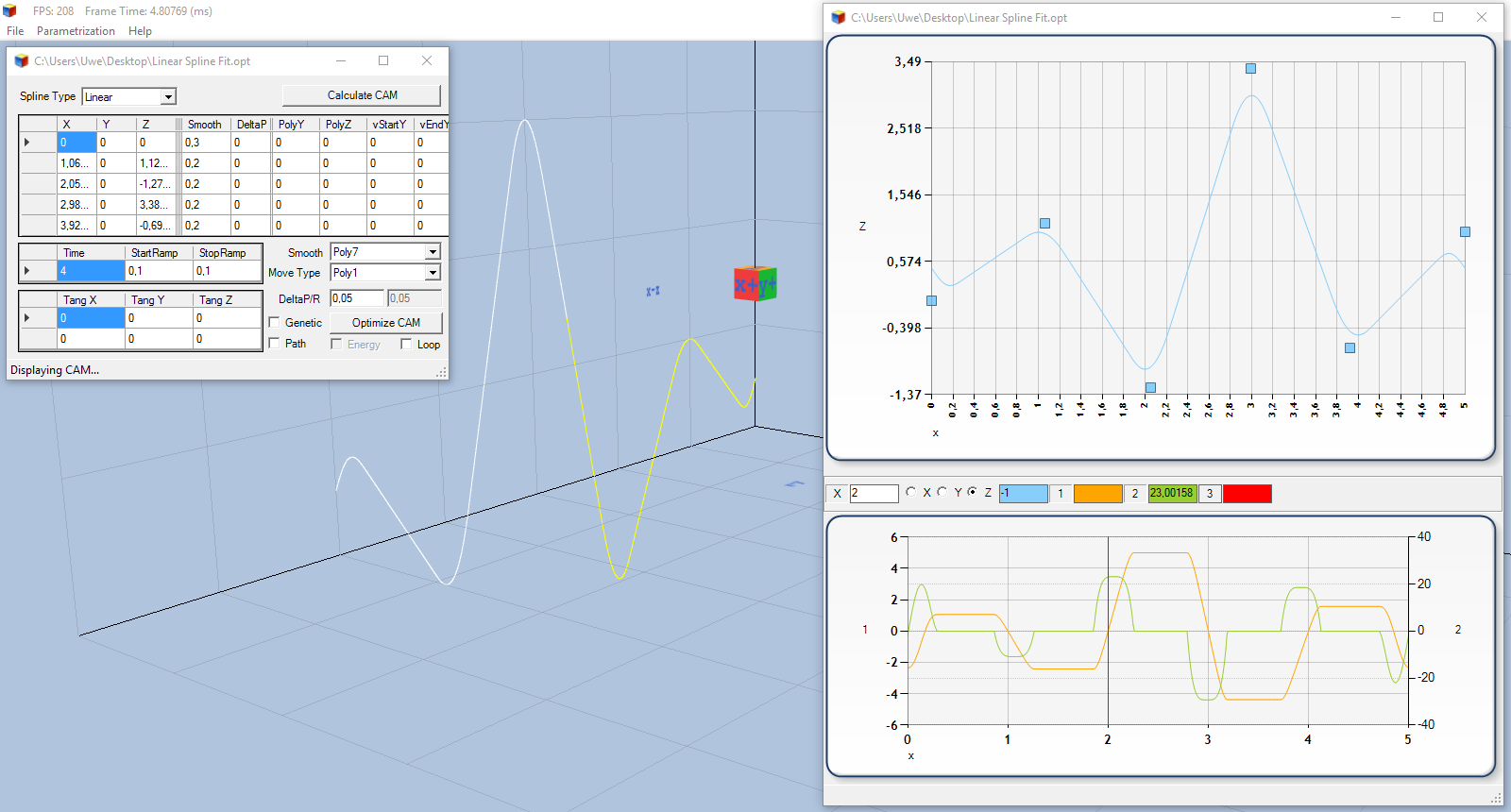
Das Video verdeutlicht, wie über die vier mittleren Umkehrpunkte (1, 1) (2, -1) (3, 3) und (4, -0.5) einfach ein Linearer Spline definiert wird und dieser dann automatisch so modifiziert wird, dass über diese Umkehrpunkte sehr dynamisch gefahren wird. Man muss an den Umkehrpunkten nicht mehr anhalten, sondern erreicht, dass die Geschwindigkeit (orange) jeweils einen Nulldurchgang aufweist und darüber hinaus kann man auch erkennen, dass zusätzlich die Beschleunigung (grün), modelliert mit einem Polynom 7. Grades, im jeweiligen Maximum gedeckelt wird.
Zur weiteren Handhabung kann der sich ergebende Lineare Spline mit Überschleifpolynomen auf jedem gängigen Motion-Control-System als Kurvenscheibe einfach abgebildet werden, sodass kein spezielles herstellerabhängiges Betriebssystem nötig ist.

