 Viele Prozesse bedingen eine dynamische punktgenaue Umkehrbewegung oder auch ein punktgenaues Überschleifen.
Viele Prozesse bedingen eine dynamische punktgenaue Umkehrbewegung oder auch ein punktgenaues Überschleifen.
Mithilfe unseres Ansatzes über Lineare Splines für die Bewegung und unsere numerischen Solver-Methoden lässt sich eine hochdynamische präzise Bewegung erzielen.
|
PGlmcmFtZSB3aWR0aD0iNTYwIiBoZWlnaHQ9IjMxNSIgc3JjPSJodHRwczovL3d3dy55b3V0dWJlLW5vY29va2llLmNvbS9lbWJlZC92V2RpVWR2SG9Bcz9yZWw9MCZhbXA7dnE9aGQxMDgwIiBmcmFtZWJvcmRlcj0iMCIgYWxsb3c9ImF1dG9wbGF5OyBlbmNyeXB0ZWQtbWVkaWEiIGFsbG93ZnVsbHNjcmVlbj0iIj48L2lmcmFtZT4= |
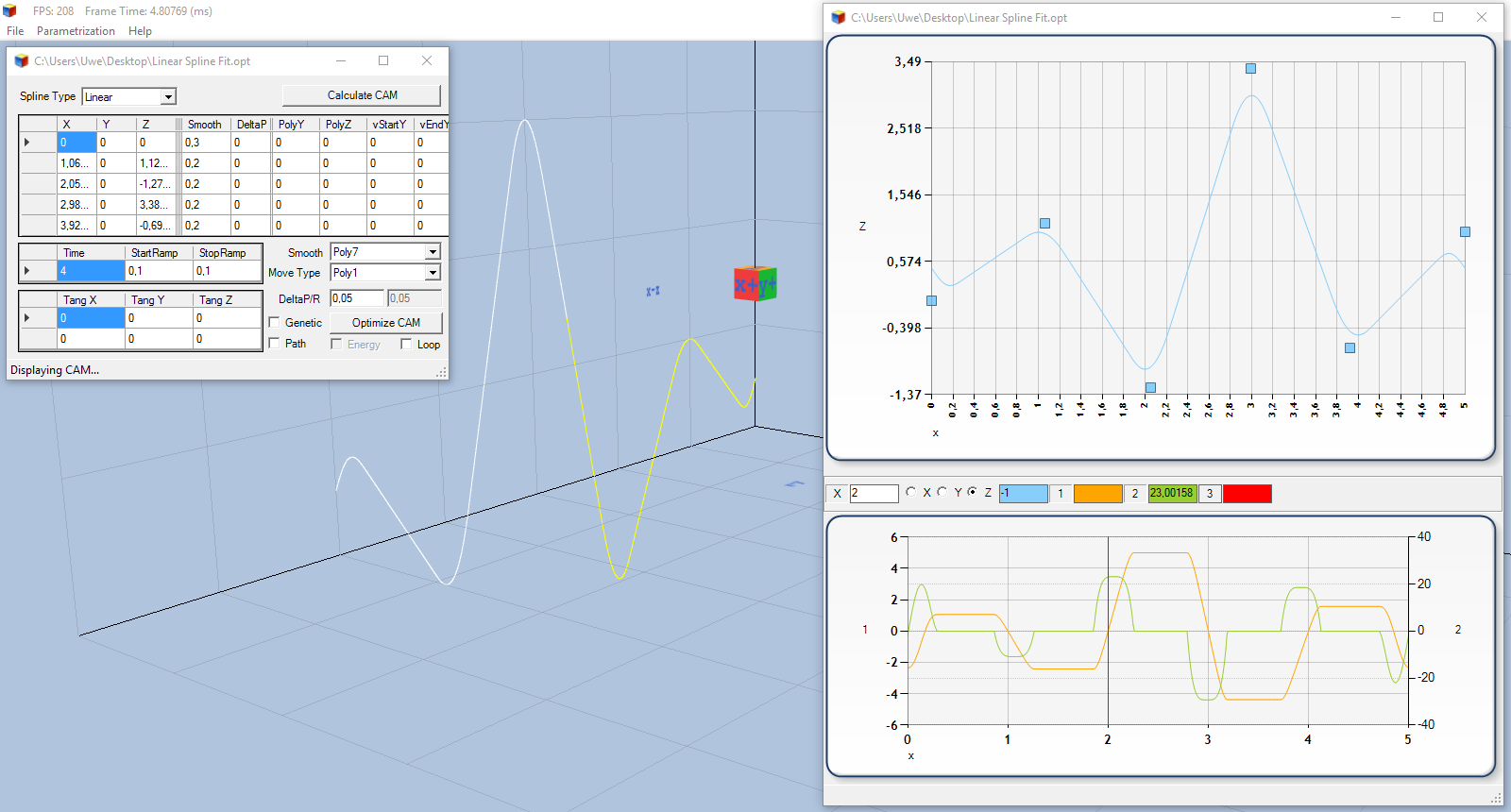
Das Video oben verdeutlicht, wie über die vier mittleren Umkehrpunkte (1, 1) (2, -1) (3, 3) und (4, -0.5) einfach ein Linearer Spline definiert wird und dieser dann automatisch so modifiziert wird, dass über diese Umkehrpunkte sehr dynamisch gefahren wird. Man muss an den Umkehrpunkten nicht mehr anhalten, sondern erreicht, dass die Geschwindigkeit (orange) jeweils einen Nulldurchgang aufweist und darüber hinaus kann man auch erkennen, dass zusätzlich die Beschleunigung (grün), modelliert mit einem Polynom 7. Grades, im jeweiligen Maximum gedeckelt wird.
Ein ähnliches Verhalten kann man auch mit Quintischen Splines erreichen, wenn man bei diesen auf eine glatte dritte Ableitung verzichtet und stattdessen an den Umkehrpunkten waagrechte Tangenten fordert, was im Video unten verdeutlicht wird.
|
PGlmcmFtZSB3aWR0aD0iNTYwIiBoZWlnaHQ9IjMxNSIgc3JjPSJodHRwczovL3d3dy55b3V0dWJlLW5vY29va2llLmNvbS9lbWJlZC95VUx4WFAwLVRRaz9yZWw9MCZhbXA7dnE9aGQxMDgwIiBmcmFtZWJvcmRlcj0iMCIgYWxsb3c9ImF1dG9wbGF5OyBlbmNyeXB0ZWQtbWVkaWEiIGFsbG93ZnVsbHNjcmVlbj0iIj48L2lmcmFtZT4= |
Zur weiteren Handhabung können sowohl sich ergebende Lineare Splines mit Überschleifpolynomen als auch Quintische Splines auf jedem gängigen Motion-Control-System als Kurvenscheibe einfach abgebildet werden, sodass kein spezielles herstellerabhängiges Betriebssystem nötig ist.
Andere Prozesse bedingen einen punktgenauen Wechsel zwischen zwei konstanten, prozess-synchronen Geschwindigkeiten. Da dies zu einem oft nicht unerheblichen Geschwindigkeitssprung führt, versuchte man bisher, solche Sprünge über geeignete Reglereinstellungen abzufangen, was dazu führte, dass der Wendepunkt nicht genau erreicht wurde.
|
PGlmcmFtZSBsb2FkaW5nPSJsYXp5IiB3aWR0aD0iNTYwIiBoZWlnaHQ9IjMxNSIgYWxpZ249ImNlbnRlciIgc3JjPSJodHRwczovL3d3dy55b3V0dWJlLW5vY29va2llLmNvbS9lbWJlZC9sbHVERC1CWmZUMD9yZWw9MCZhbXA7dnE9aGQxMDgwIiBmcmFtZWJvcmRlcj0iMCIgYWxsb3c9ImF1dG9wbGF5OyBlbmNyeXB0ZWQtbWVkaWEiIGFsbG93ZnVsbHNjcmVlbj0iIj48L2lmcmFtZT4= |
Im Video oben kann man sehr gut sehen, wie „hart“ z.B. am unteren Umkehrpunkt ohne Regelmaßnahmen gewendet wird und wie der zweite obere Wendepunkt mit reinen Regleranpassungen nicht genau erreicht wird. Wir möchten hier aber eine Lösung präsentieren, mit welcher so ein Wendemanöver auf Positionssollwertbasis mit Polynomen einfach zu realisieren ist (wie man am ersten oberen Umkehrpunkt, auf welchen die Maus zeigt, sehen kann). Der Anwender muss dabei nur den Bereich definieren, in welchem das Wendemanöver stattfinden kann und den exakten Zeitpunkt vorgeben, an welchem der Wendepunkt erreicht werden soll.
 |
Ein entsprechender Algorithmus berechnet daraus ein Wendepolynom (wahlweise 5. oder 7. Grades), welches als Kurvenscheibensegment oder als Tabelle in den Bewegungsablauf integriert werden kann. Im Bild oben sieht man, wie so ein Wendepolynom z.B. mit JetSym STX programmiert werden kann. Die Berechnung selbst dauert dabei auch auf einer kleineren Steuerung der Bucher Automation AG nur maximal ein bis zwei Millisekunden.

